FOIL Calculator

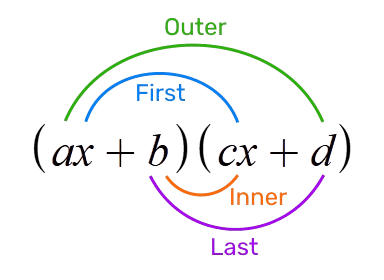
This calculator uses the first-outer-inner-last (FOIL) method to multiply two binomials. This page includes an explanation of the method as well as example computations with steps.

This diagram shows how the FOIL method is used to multiply the two binomials.

How to Use This Calculator

1. Enter the coefficients for a, b, c, and d in the input fields.

Once all coefficients are entered, the result will be computed.

Understanding the Formula

The FOIL method is used to multiply two binomials that are in this form.

The steps of FOIL are as follows:

1. First (F) - Multiply the first terms

   $ax\times cx=acx^2$

2. Outer (O) - Multiply the outer terms

   $ax\times d=adx$

3. Inner (I) - Multiply the inner terms

   $b\times cx=bcx$

4. Last (L) - Multiply the last terms

   $b\times d=bd$

5. Add the products

   $acx^2+adx+bcx+bd$

6. Combine like terms

   $acx^2+\left(ad+bc\right)x+bd$

The final result is

Example Problem

In this example, the values of the coefficients are as follows:

• a = 5
• b = 4
• c = 3
• d = 2

The steps to solve this expression:

1. First (F) - Multiply the first terms

   $ax\times cx=acx^2$$5x\times 3x=15x^2$

2. Outer (O) - Multiply the outer terms

   $ax\times d=adx$$5x\times 2=10x$

3. Inner (I) - Multiply the inner terms

   $b\times cx=bcx$$4\times 3x=12x$

4. Last (L) - Multiply the last terms

   $b\times d=bd$$4\times 2=8$

5. Add the products

   $acx^2+adx+bcx+bd$$15x^2+10x+12x+8$

6. Combine like terms

   $acx^2+\left(ad+bc\right)x+bd$$15x^2+\left(10+12\right)x+8$$15x^2+22x+8$

The final result is