AboutContact
ConversionMathPhysicsReference
AboutContact

30 60 90 Triangle Calculator

Related Calculators

45 45 90 Triangle Calculator

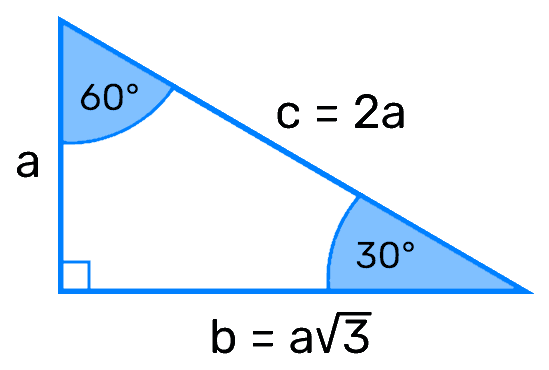
A 30 60 90 triangle showing angles and side lengths proportional to Side A

A 30 60 90 triangle is known as a special right triangle and has the angles 30°, 60°, and 90°, hence its name. You might also notice that this triangle is half of an equilateral triangle.

Right triangles are sometimes called rectangular triangles or orthogonal triangles. A triangle is a right triangle when two sides are perpendicular to each other, forming a right angle.

Because of this triangle's predictable angles, the 30 60 90 triangle calculator computes the properties of a triangle given any one of the following measurements:

  • Side (a)
  • Side (b)
  • Side (c)
  • Area
  • Perimeter

Understanding the Formula

The triangle's properties are derived from the measurement provided.

Given Side A:

b=a3b=a\sqrt{3}
c=2ac=2a
A=12abA=\frac{1}{2}ab
P=a+b+cP=a+b+c

Given Side B:

a=b3a=\frac{b}{\sqrt{3}}
c=2ac=2a
A=12abA=\frac{1}{2}ab
P=a+b+cP=a+b+c

Given Side C:

a=12ca=\frac{1}{2}c
b=a3b=a\sqrt{3}
A=12abA=\frac{1}{2}ab
P=a+b+cP=a+b+c

Given Area:

a=2A3a=\sqrt{\frac{2A}{\sqrt{3}}}
b=a3b=a\sqrt{3}
c=2ac=2a
P=a+b+cP=a+b+c

Given Perimeter:

a=P3+3a=\frac{P}{3+\sqrt{3}}
b=a3b=a\sqrt{3}
c=2ac=2a
A=12abA=\frac{1}{2}ab

Where the following variables are represented as:

  • a = Side A
  • b = Side B
  • c = Side C
  • A = Area
  • P = Perimeter

More About the Formula

Because the angles of this triangle are 30°, 60°, and 90°, we can use trigonometry to find the lengths of the other sides.

The relationship between Side A and Side C can be solved with these calculations:

a/c=sin⁡(30∘)a/c=\sin{(30^{\circ})}a/c=12a/c=\frac{1}{2}

Therefore,

c=2ac=2aa=12ca=\frac{1}{2}c

The relationship between Side B and Side C can be solved with these calculations:

b/c=sin⁡(60∘)b/c=\sin{(60^{\circ})}b/c=32b/c=\frac{\sqrt{3}}{2}

Therefore,

b=c32b=c\frac{\sqrt{3}}{2}c=2b3c=\frac{2b}{\sqrt{3}}